Le code de ce blog, ainsi que l'ensemble de données, sont disponibles sur le lien suivant https://github.com/shekharpandey89/k-means
Le clustering K-Means est un algorithme d'apprentissage automatique non supervisé. Si nous comparons l'algorithme de clustering non supervisé K-Means avec l'algorithme supervisé, il n'est pas nécessaire d'entraîner le modèle avec les données étiquetées. L'algorithme K-Means est utilisé pour classer ou regrouper différents objets en fonction de leurs attributs ou caractéristiques en un nombre K de groupes. Ici, K est un nombre entier. Le K-Means calcule la distance (à l'aide de la formule de distance), puis trouve la distance minimale entre les points de données et le cluster centroïde pour classer les données.
Comprenons les K-Means en utilisant le petit exemple en utilisant les 4 objets, et chaque objet a 2 attributs.
| Nom des objets | Attribut_X | Attribut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-Means pour résoudre l'exemple numérique :
Pour résoudre le problème numérique ci-dessus via K-Means, nous devons suivre les étapes suivantes :
L'algorithme K-Means est très simple. Tout d'abord, nous devons choisir n'importe quel nombre aléatoire de K, puis choisir les centroïdes ou le centre des clusters. Pour choisir les centroïdes, nous pouvons choisir n'importe quel nombre aléatoire d'objets pour l'initialisation (dépend de la valeur de K).
Les étapes de base de l'algorithme K-Means sont les suivantes :
- Continue de fonctionner jusqu'à ce qu'aucun objet ne bouge de son centre de gravité (stable).
- Nous choisissons d'abord des centroïdes au hasard.
- Ensuite, nous déterminons la distance entre chaque objet et les centroïdes.
- Regroupement des objets en fonction de la distance minimale.
Ainsi, chaque objet a deux points comme X et Y, et ils représentent sur l'espace graphique comme suit :
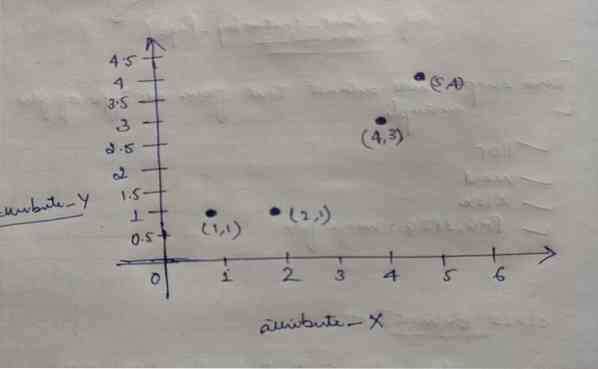
Nous choisissons donc initialement la valeur de K = 2 comme aléatoire pour résoudre notre problème ci-dessus.
Étape 1 : Initialement, nous choisissons les deux premiers objets (1, 1) et (2, 1) comme centroïdes. Le graphique ci-dessous montre la même chose. Nous appelons ces centroïdes C1 (1, 1) et C2 (2,1). Ici, on peut dire que C1 est group_1 et C2 est group_2.
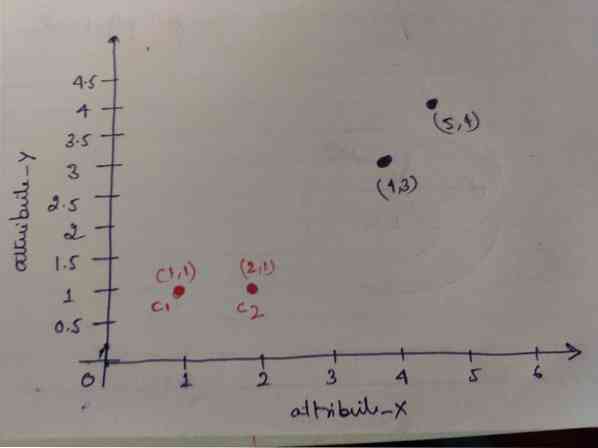
Étape 2: Maintenant, nous allons calculer chaque point de données d'objet aux centroïdes en utilisant la formule de distance euclidienne.
Pour calculer la distance, nous utilisons la formule suivante.

Nous calculons la distance entre les objets et les centroïdes, comme indiqué dans l'image ci-dessous.

Ainsi, nous avons calculé la distance de chaque point de données d'objet via la méthode de distance ci-dessus, et avons finalement obtenu la matrice de distance comme indiqué ci-dessous :
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | groupe 1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) cluster2 | groupe_2 |
| UNE | B | C | ré | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Oui |
Maintenant, nous avons calculé la valeur de distance de chaque objet pour chaque centroïde. Par exemple, les points objets (1,1) ont une valeur de distance à c1 est 0 et c2 est 1.
Comme, à partir de la matrice de distance ci-dessus, nous découvrons que l'objet (1, 1) a une distance au cluster1 (c1) est 0 et au cluster2 (c2) est 1. Donc l'objet 1 est proche du cluster1 lui-même.
De même, si nous vérifions l'objet (4, 3), la distance au cluster1 est de 3.61 et au cluster2 est 2.83. Ainsi, l'objet (4, 3) se déplacera vers cluster2.
De même, si vous recherchez l'objet (2, 1), la distance au cluster1 est 1 et au cluster2 est 0. Donc, cet objet passera à cluster2.
Maintenant, en fonction de leur valeur de distance, nous regroupons les points (groupage d'objets).
G_0 =
| UNE | B | C | ré | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | groupe 1 |
| 0 | 1 | 1 | 1 | groupe_2 |
Maintenant, selon leur valeur de distance, nous regroupons les points (groupage d'objets).
Et enfin, le graphique ressemblera à ci-dessous après avoir fait le clustering (G_0).
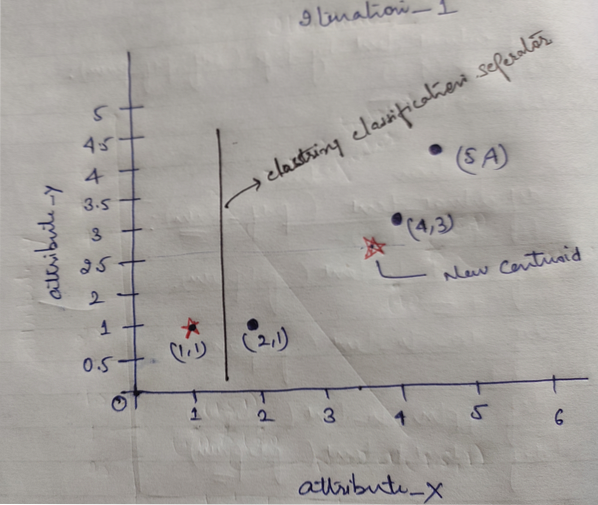
Itération_1 : Maintenant, nous allons calculer de nouveaux centroïdes lorsque les groupes initiaux ont changé en raison de la formule de distance comme indiqué dans le G_0. Ainsi, le group_1 n'a qu'un seul objet, donc sa valeur est toujours c1 (1,1), mais le group_2 a 3 objets, donc sa nouvelle valeur centroïde est 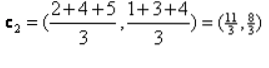
Donc, nouveaux c1 (1,1) et c2 (3.66, 2.66)
Maintenant, nous devons à nouveau calculer toute la distance aux nouveaux centroïdes comme nous l'avons calculé auparavant.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | groupe 1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) cluster2 | groupe_2 |
| UNE | B | C | ré | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Oui |
Itération_1 (regroupement d'objets) : Maintenant, au nom du nouveau calcul de la matrice de distance (DM_1), nous le regroupons en fonction de cela. Donc, nous déplaçons l'objet M2 de group_2 à group_1 comme règle de distance minimale aux centroïdes, et le reste de l'objet sera le même. Donc, le nouveau cluster sera comme ci-dessous.
G_1 =
| UNE | B | C | ré | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | groupe 1 |
| 0 | 0 | 1 | 1 | groupe_2 |
Maintenant, nous devons recalculer les nouveaux centroïdes, car les deux objets ont deux valeurs.
Ainsi, de nouveaux centroïdes seront 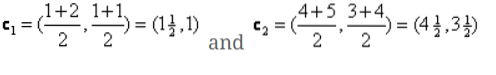
Ainsi, après avoir obtenu les nouveaux centroïdes, le regroupement ressemblera à ci-dessous :
c1 = (1.5, 1)
c2 = (4.5, 3.5)
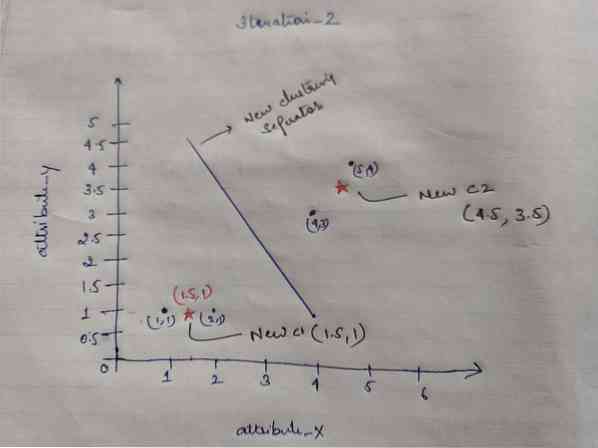
Itération_2 : Nous répétons l'étape où nous calculons la nouvelle distance de chaque objet aux nouveaux centroïdes calculés. Ainsi, après le calcul, nous obtiendrons la matrice de distance suivante pour iteration_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) cluster1 | groupe 1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) cluster2 | groupe_2 |
A B C D
| UNE | B | C | ré | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Oui |
Encore une fois, nous effectuons les affectations de regroupement en fonction de la distance minimale comme nous le faisions auparavant. Donc, après avoir fait cela, nous avons obtenu la matrice de clustering qui est la même que G_1.
G_2 =
| UNE | B | C | ré | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | groupe 1 |
| 0 | 0 | 1 | 1 | groupe_2 |
Comme ici, G_2 == G_1, donc aucune autre itération n'est requise, et nous pouvons nous arrêter ici.
Implémentation de K-Means à l'aide de Python :
Maintenant, nous allons implémenter l'algorithme K-means en python. Pour implémenter les K-means, nous allons utiliser le célèbre jeu de données Iris, qui est open-source. Cet ensemble de données a trois classes différentes. Cet ensemble de données a essentiellement quatre caractéristiques : Longueur des sépales, largeur des sépales, longueur des pétales et largeur des pétales. La dernière colonne dira le nom de la classe de cette ligne comme setosa.
L'ensemble de données ressemble à ce qui suit :
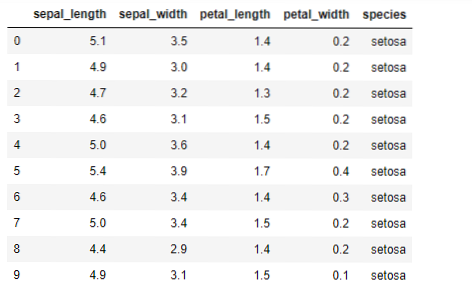
Pour l'implémentation python k-means, nous devons importer les bibliothèques requises. Nous importons donc Pandas, Numpy, Matplotlib, et aussi KMeans depuis sklearn.encombrement comme indiqué ci-dessous :

Nous lisons l'Iris.csv en utilisant la méthode read_csv panda et affichera les 10 premiers résultats en utilisant la méthode head.
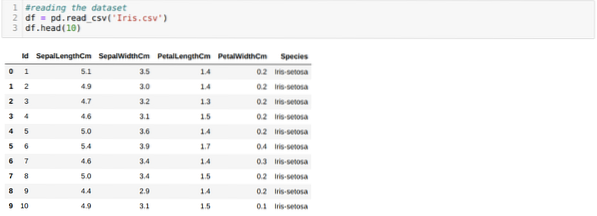
Maintenant, nous ne lisons que les caractéristiques de l'ensemble de données dont nous avons besoin pour entraîner le modèle. Nous lisons donc les quatre caractéristiques des ensembles de données (longueur des sépales, largeur des sépales, longueur des pétales, largeur des pétales). Pour cela, nous avons passé les quatre valeurs d'index [0, 1, 2, 3] dans la fonction iloc de la trame de données du panda (df) comme indiqué ci-dessous :
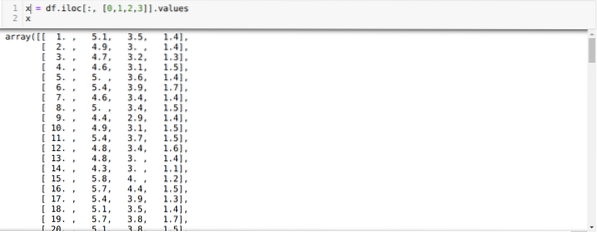
Maintenant, nous choisissons le nombre de clusters au hasard (K=5). Nous créons l'objet de la classe K-means, puis adaptons notre ensemble de données x à celui-ci pour l'entraînement et la prédiction, comme indiqué ci-dessous :
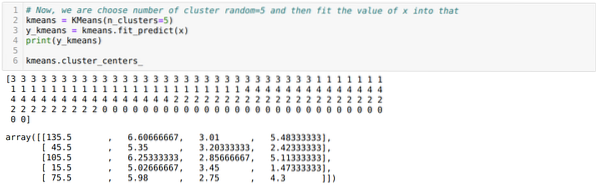
Maintenant, nous allons visualiser notre modèle avec la valeur aléatoire K=5. Nous pouvons clairement voir cinq clusters, mais il semble que ce ne soit pas exact, comme indiqué ci-dessous.
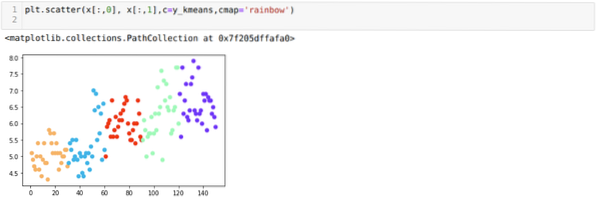
Notre prochaine étape consiste donc à déterminer si le nombre de grappes était exact ou non. Et pour cela, nous utilisons la méthode Elbow. La méthode Elbow est utilisée pour trouver le nombre optimal du cluster pour un jeu de données particulier. Cette méthode sera utilisée pour savoir si la valeur de k=5 était correcte ou non car nous n'obtenons pas de clustering clair. Donc après cela, nous passons au graphique suivant, qui montre que la valeur de K=5 n'est pas correcte car la valeur optimale se situe entre 3 ou 4.
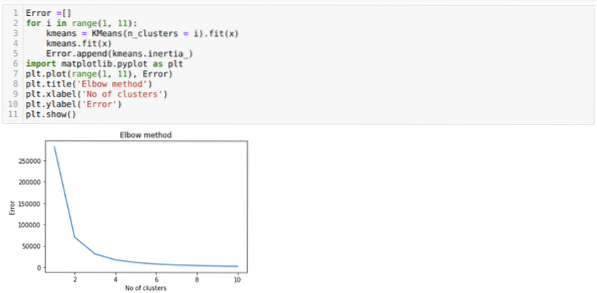
Maintenant, nous allons réexécuter le code ci-dessus avec le nombre de clusters K=4 comme indiqué ci-dessous :
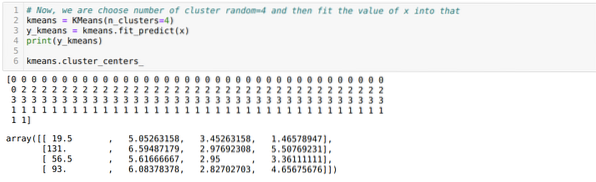
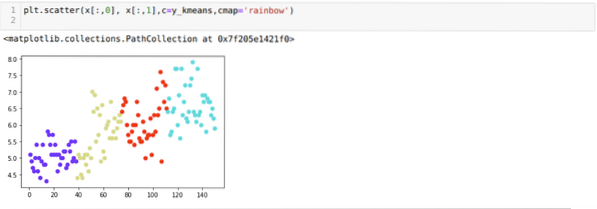
Maintenant, nous allons visualiser le clustering de nouvelles versions K = 4 ci-dessus. L'écran ci-dessous montre que maintenant le clustering se fait via les k-means.
Conclusion
Ainsi, nous avons étudié l'algorithme K-means dans le code numérique et python. Nous avons également vu comment nous pouvons connaître le nombre de clusters pour un ensemble de données particulier. Parfois, la méthode Elbow ne peut pas donner le bon nombre de clusters, donc dans ce cas, il y a plusieurs méthodes que nous pouvons choisir.
 Phenquestions
Phenquestions


