Dans l'ensemble, nous aborderons trois sujets principaux dans cette leçon :
- Que sont les Tensors et TensorFlow
- Appliquer des algorithmes de ML avec TensorFlow
- Cas d'utilisation de TensorFlow
TensorFlow est un excellent package Python de Google qui fait bon usage du paradigme de programmation de flux de données pour des calculs mathématiques hautement optimisés. Certaines des fonctionnalités de TensorFlow sont :
- Capacité de calcul distribuée qui facilite la gestion des données dans de grands ensembles
- L'apprentissage en profondeur et la prise en charge du réseau neuronal sont bons
- Il gère très efficacement les structures mathématiques complexes comme les tableaux à n dimensions
En raison de toutes ces fonctionnalités et de la gamme d'algorithmes d'apprentissage automatique mis en œuvre par TensorFlow, cela en fait une bibliothèque à l'échelle de la production. Plongeons-nous dans les concepts de TensorFlow afin que nous puissions nous salir les mains avec le code juste après.
Installer TensorFlow
Comme nous utiliserons l'API Python pour TensorFlow, il est bon de savoir qu'elle fonctionne à la fois avec Python 2.7 et 3.3+ versions. Installons la bibliothèque TensorFlow avant de passer aux exemples et concepts réels. Il y a deux façons d'installer ce paquet. Le premier inclut l'utilisation du gestionnaire de packages Python, pip :
pip installer tensorflowLa deuxième manière concerne Anaconda, nous pouvons installer le package en tant que :
conda install -c conda-forge tensorflowN'hésitez pas à rechercher les versions nocturnes et les versions GPU sur les pages d'installation officielles de TensorFlow.
J'utiliserai le gestionnaire Anaconda pour tous les exemples de cette leçon. Je vais lancer un Jupyter Notebook pour le même :

Maintenant que nous sommes prêts avec toutes les instructions d'importation pour écrire du code, commençons à plonger dans le package SciPy avec quelques exemples pratiques.
Que sont les tenseurs?
Les tenseurs sont les structures de données de base utilisées dans Tensorflow. Oui, ils ne sont qu'un moyen de représenter les données dans le deep learning. Visualisons-les ici :
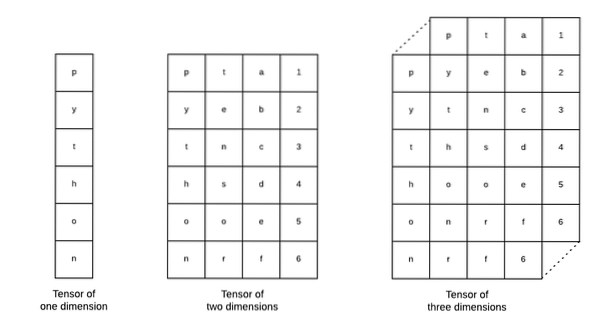
Comme décrit dans l'image, les tenseurs peuvent être qualifiés de tableau à n dimensions qui nous permet de représenter des données dans une dimension complexe. Nous pouvons considérer chaque dimension comme une caractéristique différente des données dans l'apprentissage en profondeur. Cela signifie que les Tensors peuvent devenir assez complexes lorsqu'il s'agit d'ensembles de données complexes avec de nombreuses fonctionnalités.
Une fois que nous savons ce que sont les Tensors, je pense qu'il est assez facile de dériver ce qui se passe dans TensorFlow. Ces termes signifient comment les tenseurs ou les entités peuvent circuler dans les ensembles de données pour produire une sortie précieuse lorsque nous effectuons diverses opérations dessus.
Comprendre TensorFlow avec des constantes
Tout comme nous l'avons lu ci-dessus, TensorFlow nous permet d'effectuer des algorithmes d'apprentissage automatique sur les Tensors pour produire une sortie précieuse. Avec TensorFlow, la conception et la formation de modèles d'apprentissage profond sont simples.
TensorFlow est livré avec la construction Graphiques de calcul. Les graphiques de calcul sont des graphiques de flux de données dans lesquels les opérations mathématiques sont représentées sous forme de nœuds et les données sont représentées sous forme de bords entre ces nœuds. Écrivons un extrait de code très simple pour fournir une visualisation concrète :
importer tensorflow en tant que tfx = vf.constante(5)
y = tf.constante(6)
z = x * y
imprimer(z)
Lorsque nous exécutons cet exemple, nous verrons la sortie suivante :
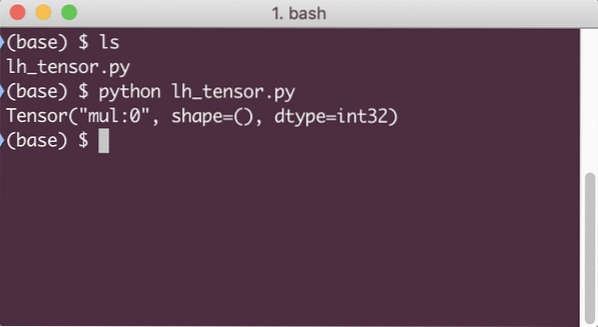
Pourquoi la multiplication est-elle fausse? Ce n'était pas ce à quoi nous nous attendions. Cela s'est produit parce que ce n'est pas ainsi que nous pouvons effectuer des opérations avec TensorFlow. Tout d'abord, nous devons commencer un session pour que le graphe de calcul fonctionne,
Avec Sessions, nous pouvons encapsuler le contrôle des opérations et de l'état des Tenseurs. Cela signifie qu'une session peut également stocker le résultat d'un graphe de calcul afin qu'elle puisse passer ce résultat à l'opération suivante dans l'ordre d'exécution des pipelines. Créons maintenant une session pour obtenir le résultat correct :
# Commencer par l'objet sessionsession = tf.Session()
# Fournir le calcul à la session et le stocker
résultat = séance.exécuter(z)
# Imprimer le résultat du calcul
imprimer (résultat)
# Fermer la session
session.Fermer()
Cette fois, nous avons obtenu la session et lui avons fourni le calcul dont elle a besoin pour s'exécuter sur les nœuds. Lorsque nous exécutons cet exemple, nous verrons la sortie suivante :
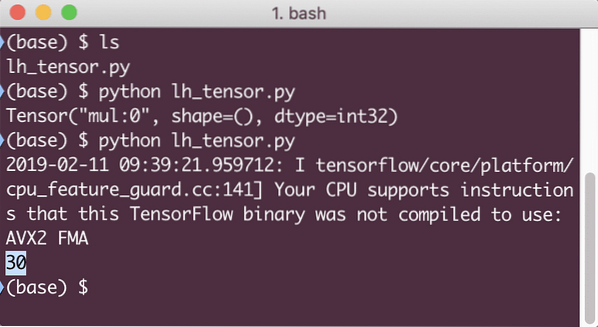
Bien que nous ayons reçu un avertissement de TensorFlow, nous avons toujours obtenu la sortie correcte du calcul.
Opérations tensorielles à élément unique
Tout comme nous avons multiplié deux Tensors constants dans le dernier exemple, nous avons de nombreuses autres opérations dans TensorFlow qui peuvent être effectuées sur des éléments uniques :
- ajouter
- soustraire
- multiplier
- div
- mode
- abdos
- négatif
- signe
- carré
- rond
- carré
- pow
- exp
- Journal
- maximum
- le minimum
- car
- péché
Les opérations à élément unique signifient que même lorsque vous fournissez un tableau, les opérations seront effectuées sur chacun des éléments de ce tableau. Par example:
importer tensorflow en tant que tfimporter numpy en tant que np
tenseur = np.tableau([2, 5, 8])
tenseur = tf.convert_to_tensor(tenseur, dtype=tf.float64)
avec tf.Session() en tant que session :
imprimer (session.courir(tf.cos(tenseur)))
Lorsque nous exécutons cet exemple, nous verrons la sortie suivante :
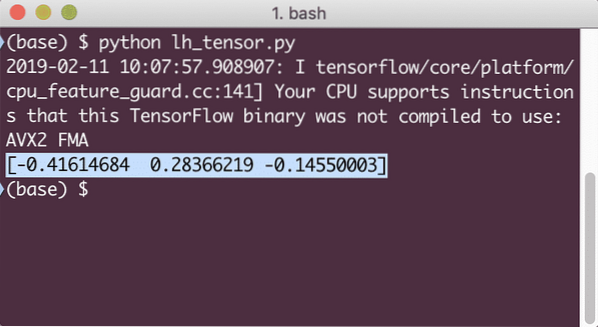
Nous avons compris ici deux concepts importants :
- Tout tableau NumPy peut être facilement converti en un tenseur à l'aide de la fonction convert_to_tensor
- L'opération a été effectuée sur chacun des éléments du tableau NumPy
Espaces réservés et variables
Dans l'une des sections précédentes, nous avons examiné comment utiliser les constantes Tensorflow pour créer des graphiques de calcul. Mais TensorFlow nous permet également de prendre des entrées à la volée afin que le graphique de calcul puisse être de nature dynamique. Ceci est possible avec l'aide des espaces réservés et des variables.
En réalité, les espaces réservés ne contiennent aucune donnée et doivent recevoir des entrées valides pendant l'exécution et comme prévu, sans entrée, ils généreront une erreur.
Un espace réservé peut être qualifié d'accord dans un graphique selon lequel une entrée sera sûrement fournie au moment de l'exécution. Voici un exemple d'espaces réservés :
importer tensorflow en tant que tf# Deux espaces réservés
x = vf. espace réservé(tf.float32)
y = tf. espace réservé(tf.float32)
# Affectation de l'opération de multiplication w.r.t. une & b au nœud mul
z = x * y
# Créer une session
session = tf.Session()
# Valeurs de passage pour les espaces réservés
résultat = séance.exécuter(z, x : [2, 5], y : [3, 7])
print('Multiplication de x et y :', résultat)
Lorsque nous exécutons cet exemple, nous verrons la sortie suivante :
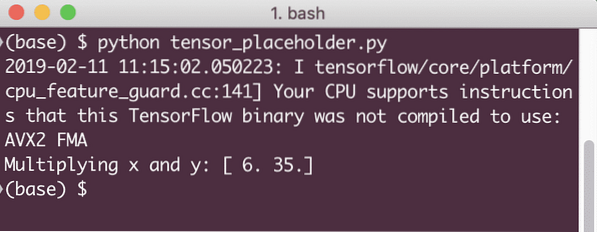
Maintenant que nous avons des connaissances sur les espaces réservés, tournons notre attention vers les variables. Nous savons que la sortie d'une équation peut changer pour le même ensemble d'entrées au fil du temps. Ainsi, lorsque nous formons notre variable de modèle, elle peut changer son comportement au fil du temps. Dans ce scénario, une variable nous permet d'ajouter ces paramètres entraînables à notre graphe de calcul. Une variable peut être définie comme suit :
x = vf.Variable( [5.2], dtype = tf.float32 )Dans l'équation ci-dessus, x est une variable qui reçoit sa valeur initiale et le type de données. Si nous ne fournissons pas le type de données, il sera déduit par TensorFlow avec sa valeur initiale. Reportez-vous aux types de données TensorFlow ici.
Contrairement à une constante, nous devons appeler une fonction Python pour initialiser toutes les variables d'un graphe :
init = tf.global_variables_initializer()session.exécuter (initialiser)
Assurez-vous d'exécuter la fonction TensorFlow ci-dessus avant d'utiliser notre graphique.
Régression linéaire avec TensorFlow
La régression linéaire est l'un des algorithmes les plus couramment utilisés pour établir une relation dans une donnée continue donnée. Cette relation entre les points de coordonnées, disons x et y, est appelée un hypothèse. Quand on parle de régression linéaire, l'hypothèse est une ligne droite :
y = mx + cIci, m est la pente de la droite et ici, c'est un vecteur représentant poids. c est le coefficient constant (ordonnée à l'origine) et ici, il représente le Biais. Le poids et le biais sont appelés les paramètres du modèle.
Les régressions linéaires nous permettent d'estimer les valeurs de poids et de biais telles que nous ayons un minimum fonction de coût. Enfin, le x est la variable indépendante dans l'équation et y est la variable dépendante. Commençons maintenant à créer le modèle linéaire dans TensorFlow avec un simple extrait de code que nous allons expliquer :
importer tensorflow en tant que tf# Variables pour la pente du paramètre (W) avec une valeur initiale de 1.1
W = tf.Variable([1.1], vf.float32)
# Variable pour le biais (b) avec une valeur initiale de -1.1
b = vf.Variable([-1.1], vf.float32)
# Espaces réservés pour fournir une entrée ou une variable indépendante, désignés par x
x = vf.espace réservé(tf.float32)
# Equation de la ligne ou la régression linéaire
modèle_linéaire = W * x + b
# Initialisation de toutes les variables
session = tf.Session()
init = tf.global_variables_initializer()
session.exécuter (initialiser)
# Exécuter le modèle de régression
imprimer (session.run(linear_model x: [2, 5, 7, 9]))
Ici, nous avons fait exactement ce que nous avons expliqué plus tôt, résumons ici :
- Nous avons commencé par importer TensorFlow dans notre script
- Créez des variables pour représenter le poids du vecteur et le biais du paramètre
- Un espace réservé sera nécessaire pour représenter l'entrée, x
- Représenter le modèle linéaire
- Initialiser toutes les valeurs nécessaires au modèle
Lorsque nous exécutons cet exemple, nous verrons la sortie suivante :
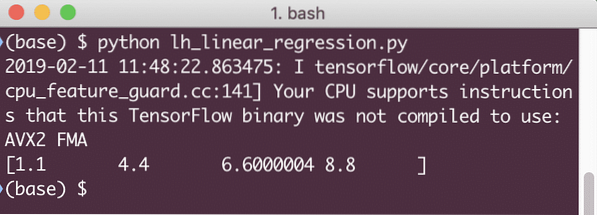
L'extrait de code simple fournit juste une idée de base sur la façon dont nous pouvons construire un modèle de régression. Mais nous devons encore faire quelques étapes supplémentaires pour compléter le modèle que nous avons construit :
- Nous devons rendre notre modèle auto-formable afin qu'il puisse produire une sortie pour n'importe quelle entrée donnée
- Nous devons valider la sortie fournie par le modèle en la comparant à la sortie attendue pour x donné
Fonction de perte et validation du modèle
Pour valider le modèle, nous devons avoir une mesure de la déviation de la sortie actuelle par rapport à la sortie attendue. Il existe diverses fonctions de perte qui peuvent être utilisées ici pour la validation, mais nous examinerons l'une des méthodes les plus courantes, Somme des erreurs au carré ou SSE.
L'équation de la SSE est donnée par :
E = 1/2 * (t - y)2Ici:
- E = erreur quadratique moyenne
- t = sortie reçue
- y = sortie attendue
- t - y = Erreur
Maintenant, écrivons un extrait de code dans la continuité du dernier extrait pour refléter la valeur de perte :
y = tf.espace réservé(tf.float32)erreur = modèle_linéaire - y
squared_errors = tf.carré (erreur)
perte = tf.reduce_sum(squared_errors)
imprimer (session.exécuter(perte, x:[2, 5, 7, 9], y:[2, 4, 6, 8]))
Lorsque nous exécutons cet exemple, nous verrons la sortie suivante :
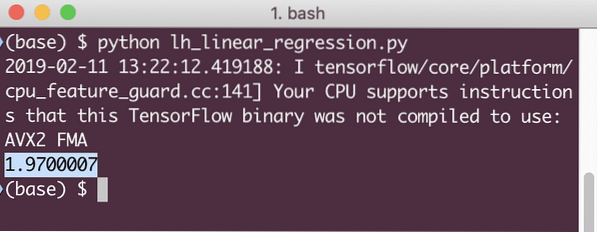
De toute évidence, la valeur de perte est très faible pour le modèle de régression linéaire donné.
Conclusion
Dans cette leçon, nous avons examiné l'un des packages d'apprentissage profond et d'apprentissage automatique les plus populaires, TensorFlow. Nous avons également fait un modèle de régression linéaire qui avait une très grande précision.
 Phenquestions
Phenquestions