La bibliothèque NumPy nous permet d'effectuer diverses opérations qui doivent être effectuées sur des structures de données souvent utilisées dans l'apprentissage automatique et la science des données comme les vecteurs, les matrices et les tableaux. Nous ne montrerons que les opérations les plus courantes avec NumPy qui sont utilisées dans de nombreux pipelines de Machine Learning. Enfin, veuillez noter que NumPy n'est qu'un moyen d'effectuer les opérations, donc, les opérations mathématiques que nous montrons sont l'objectif principal de cette leçon et non le package NumPy lui-même. Commençons.
Qu'est-ce qu'un vecteur?
Selon Google, un vecteur est une quantité ayant une direction ainsi qu'une magnitude, notamment pour déterminer la position d'un point dans l'espace par rapport à un autre.
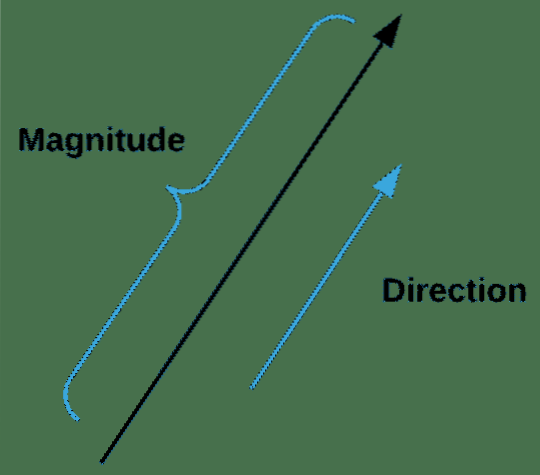
Les vecteurs sont très importants dans l'apprentissage automatique car ils décrivent non seulement la magnitude, mais aussi la direction des caractéristiques. Nous pouvons créer un vecteur dans NumPy avec l'extrait de code suivant :
importer numpy en tant que npvecteur_ligne = np.tableau([1,2,3])
print(ligne_vecteur)
Dans l'extrait de code ci-dessus, nous avons créé un vecteur de ligne. Nous pouvons également créer un vecteur colonne comme :
importer numpy en tant que npvecteur_col = np.tableau([[1],[2],[3]])
print(col_vector)
Faire une matrice
Une matrice peut être simplement comprise comme un tableau à deux dimensions. Nous pouvons créer une matrice avec NumPy en créant un tableau multidimensionnel :
matrice = np.tableau([[1, 2, 3], [4, 5, 6], [7, 8, 9]])imprimer (matrice)
Bien que la matrice soit exactement similaire au tableau multidimensionnel, la structure de données matricielle n'est pas recommandée pour deux raisons :
- Le tableau est la norme en ce qui concerne le package NumPy
- La plupart des opérations avec NumPy renvoient des tableaux et non une matrice
Utiliser une matrice creuse
Pour rappel, une matrice creuse est celle dans laquelle la plupart des items sont nuls. Maintenant, un scénario courant dans le traitement des données et l'apprentissage automatique consiste à traiter des matrices dans lesquelles la plupart des éléments sont nuls. Par exemple, considérons une matrice dont les lignes décrivent chaque vidéo sur Youtube et les colonnes représentent chaque utilisateur enregistré. Chaque valeur représente si l'utilisateur a regardé une vidéo ou non. Bien sûr, la majorité des valeurs de cette matrice seront nulles. le avantage avec une matrice creuse c'est qu'il ne stocke pas les valeurs qui sont nulles. Il en résulte un énorme avantage de calcul et une optimisation du stockage ainsi.
Créons une matrice d'étincelles ici :
de scipy importation clairseméematrice_origine = np.tableau([[1, 0, 3], [0, 0, 6], [7, 0, 0]])
sparse_matrix = clairsemé.csr_matrix(original_matrix)
imprimer(sparse_matrix)
Pour comprendre le fonctionnement du code, nous allons examiner la sortie ici :
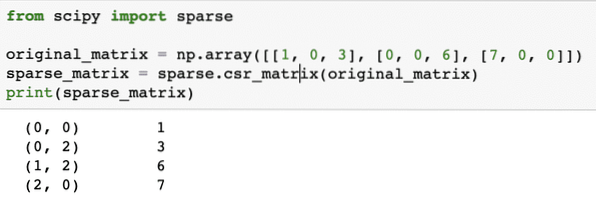
Dans le code ci-dessus, nous avons utilisé une fonction NumPy pour créer un Ligne clairsemée compressée matrice où les éléments non nuls sont représentés à l'aide des index de base zéro. Il existe différents types de matrice creuse, comme :
- Colonne creuse compressée
- Liste des listes
- Dictionnaire des clés
Nous ne plongerons pas dans d'autres matrices clairsemées ici, mais sachez que chacune de leurs utilisations est spécifique et que personne ne peut être qualifié de « meilleur ».
Application d'opérations à tous les éléments vectoriels
C'est un scénario courant lorsque nous devons appliquer une opération commune à plusieurs éléments vectoriels. Cela peut être fait en définissant un lambda puis en vectorisant le même. Voyons un extrait de code pour la même chose :
matrice = np.déployer([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
mul_5 = lambda x : x * 5
vectorized_mul_5 = np.vectoriser(mul_5)
vectorized_mul_5(matrice)
Pour comprendre comment fonctionne le code, nous allons regarder la sortie ici :

Dans l'extrait de code ci-dessus, nous avons utilisé la fonction vectorize qui fait partie de la bibliothèque NumPy, pour transformer une simple définition lambda en une fonction qui peut traiter chaque élément du vecteur. Il est important de noter que vectoriser est juste une boucle sur les éléments et cela n'a aucun effet sur la performance du programme. NumPy permet également diffusion, ce qui signifie qu'au lieu du code complexe ci-dessus, nous aurions pu simplement faire :
matrice * 5Et le résultat aurait été exactement le même. Je voulais d'abord montrer la partie complexe, sinon vous auriez sauté la section!
Moyenne, variance et écart type
Avec NumPy, il est facile d'effectuer des opérations liées aux statistiques descriptives sur les vecteurs. La moyenne d'un vecteur peut être calculée comme :
np.moyenne (matrice)La variance d'un vecteur peut être calculée comme :
np.var(matrice)L'écart type d'un vecteur peut être calculé comme suit :
np.std(matrice)La sortie des commandes ci-dessus sur la matrice donnée est donnée ici :

Transposer une matrice
La transposition est une opération très courante dont vous entendrez parler chaque fois que vous serez entouré de matrices. La transposition n'est qu'un moyen d'échanger les valeurs de colonnes et de lignes d'une matrice. Veuillez noter qu'un le vecteur ne peut pas être transposé car un vecteur n'est qu'une collection de valeurs sans que ces valeurs soient classées en lignes et en colonnes. Veuillez noter que la conversion d'un vecteur ligne en vecteur colonne n'est pas une transposition (basée sur les définitions de l'algèbre linéaire, ce qui sort du cadre de cette leçon).
Pour l'instant, on va trouver la paix juste en transposant une matrice. Il est très simple d'accéder à la transposition d'une matrice avec NumPy :
matrice.TLa sortie de la commande ci-dessus sur la matrice donnée est donnée ici :
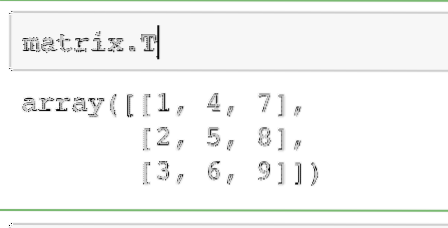
La même opération peut être effectuée sur un vecteur ligne pour le convertir en vecteur colonne.
Aplatir une matrice
Nous pouvons convertir une matrice en un tableau à une dimension si nous souhaitons traiter ses éléments de manière linéaire. Cela peut être fait avec l'extrait de code suivant :
matrice.aplatir()La sortie de la commande ci-dessus sur la matrice donnée est donnée ici :

Notez que la matrice aplatie est un tableau à une dimension, simplement linéaire à la mode.
Calcul des valeurs propres et des vecteurs propres
Les vecteurs propres sont très couramment utilisés dans les packages de Machine Learning. Ainsi, lorsqu'une fonction de transformation linéaire est présentée sous forme de matrice, alors X, les vecteurs propres sont les vecteurs qui changent uniquement d'échelle du vecteur mais pas sa direction. On peut dire ça:
Xv = vIci, X est la matrice carrée et γ contient les valeurs propres. De plus, v contient les vecteurs propres. Avec NumPy, il est facile de calculer les valeurs propres et les vecteurs propres. Voici l'extrait de code où nous démontrons la même chose :
evalues, evectors = np.linalg.eig(matrice)La sortie de la commande ci-dessus sur la matrice donnée est donnée ici :
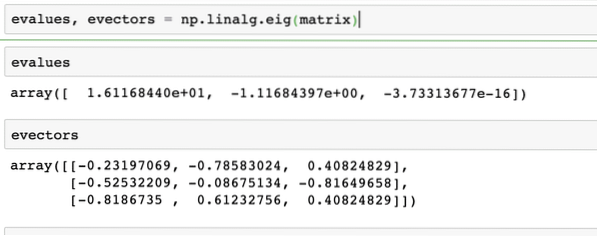
Produits de points de vecteurs
Dot Products of Vectors est un moyen de multiplier 2 vecteurs. Il vous parle de combien de vecteurs sont dans la même direction, par opposition au produit vectoriel qui vous dit le contraire, combien peu les vecteurs sont dans la même direction (appelé orthogonal). Nous pouvons calculer le produit scalaire de deux vecteurs comme indiqué dans l'extrait de code ici :
a = np.tableau([3, 5, 6])b = np.tableau([23, 15, 1])
np.point(a, b)
La sortie de la commande ci-dessus sur les tableaux donnés est donnée ici :

Ajouter, soustraire et multiplier des matrices
L'ajout et la soustraction de plusieurs matrices est une opération assez simple dans les matrices. Il y a deux façons de le faire. Regardons l'extrait de code pour effectuer ces opérations. Dans le but de garder cela simple, nous utiliserons deux fois la même matrice :
np.ajouter(matrice, matrice)Ensuite, deux matrices peuvent être soustraites comme :
np.soustraire(matrice, matrice)La sortie de la commande ci-dessus sur la matrice donnée est donnée ici :
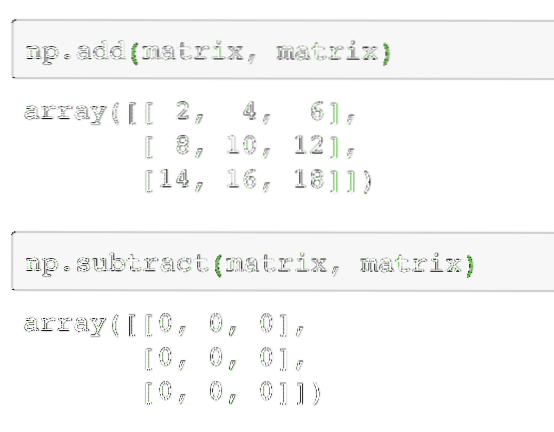
Comme prévu, chacun des éléments de la matrice est ajouté/soustrait avec l'élément correspondant. La multiplication d'une matrice est similaire à la recherche du produit scalaire comme nous l'avons fait précédemment :
np.point(matrice, matrice)Le code ci-dessus trouvera la vraie valeur de multiplication de deux matrices, donnée par :
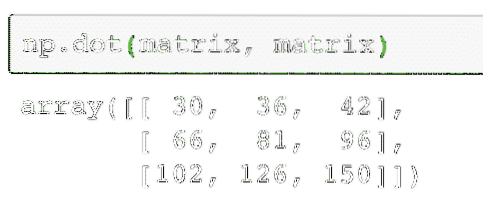
La sortie de la commande ci-dessus sur la matrice donnée est donnée ici :

Conclusion
Dans cette leçon, nous avons parcouru de nombreuses opérations mathématiques liées aux vecteurs, aux matrices et aux tableaux qui sont couramment utilisés. Traitement des données, statistiques descriptives et science des données. Il s'agissait d'une leçon rapide couvrant uniquement les sections les plus courantes et les plus importantes de la grande variété de concepts, mais ces opérations devraient donner une très bonne idée de ce que toutes les opérations peuvent être effectuées tout en traitant ces structures de données.
Veuillez partager librement vos commentaires sur la leçon sur Twitter avec @linuxhint et @sbmaggarwal (c'est moi!).
 Phenquestions
Phenquestions